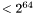symbolism::ring::N

N Class Reference

Arbitrarily large natural numbers (positive integers including zero). More...

#include <symbolism/N.h>

List of all members.

Members

typedef mp_limb_t limb_t
 The type of the digits in the large number.
typedef long unsigned int size_t
 The type of the arrays size.
static const int bits_per_limb = 8 * sizeof(limb_t)
 Constant representing the number of bits in a limb_t.
size_t size
 The number of limbs minus one.
union {
   limb_t   limb
 If size is zero then limb contains the entire integer.
   limb_t *   data
 Array of limbs representing the integer. If size >= 1 then data will contain an allocated array of size + 1 limbs representing the integer from least significant limb data[0] to the most significant limb data[size].
}; 

Constructors and Destructors

 N ()
 N (const N &copy)
 N (const limb_t value)
 ~N ()

Basic operations

limb_t * limbs ()
const limb_t * limbs () const
void set (const N &copy)
void set (const limb_t value)
N & operator= (const N &copy)
N & operator= (const limb_t value)
void reserve (size_t newsize)
 Reserve space for newsize limbs.
void resize (size_t newsize)
 Resize the integer to use newsize limbs.
void truncate (size_t newsize)
 Truncate the integer to use newsize limbs.
void normalize ()
 Normalize the number.
void swap (N &a, N &b)
size_t max (const size_t a, const size_t b)
 Returns the greatest of two N::size_t's.

Comparisson operations

bool is_zero () const
bool is_one () const
int compare (const N &a) const
int compare (const limb_t a) const
bool operator== (const N &a, const N &b)
bool operator!= (const N &a, const N &b)
bool operator> (const N &a, const N &b)
bool operator>= (const N &a, const N &b)
bool operator< (const N &a, const N &b)
bool operator<= (const N &a, const N &b)

Binary operations

size_t two_multiplicity () const
 Returns the number of trailing zeros in the binary representation.
void binary_not (const N &a)
void binary_not ()
void binary_and (const N &a, const N &b)
void binary_and (const N &a)
void binary_or (const N &a, const N &b)
void binary_or (const N &a)
void binary_xor (const N &a, const N &b)
void binary_xor (const N &a)
void left_shift (const N &a, unsigned int count)
void left_shift (unsigned int count)
void right_shift (const N &a, unsigned int count)
void right_shift (unsigned int count)
N & operator<<= (const limb_t count)
N & operator>>= (const limb_t cout)
N & operator &= (const N &a)
N & operator|= (const N &a)
N operator~ (const N &a)
N operator & (const N &a, const N &b)
N operator| (const N &a, const N &b)
N operator<< (const N &a, unsigned int count)
N operator>> (const N &a, unsigned int count)

Addition operations

void add (const N &a, const N &b)
void add (const N &a)
void add_one ()
N & operator+= (const N &rhs)
N & operator++ ()
N operator++ (int)
N operator+ (const N &a, const N &b)

Substraction operations

void sub (const N &a, const N &b)
void sub (const N &a)
void sub_one ()
N & operator-= (const N &rhs)
N & operator-- ()
N operator-- (int)
N operator- (const N &a, const N &b)

Multiplication operations

void mul (const N &a, const N &b)
void mul (const N &a)
N & operator *= (const N &rhs)
N operator * (const N &a, const N &b)

Combined addition and multiplication operations

void addmul (const N &a, const limb_t b)
void submul (const N &a, const limb_t b)

Division operations

void exact_div (const N &a, const N &b)
void exact_div (const N &a)
void div (N &rem, const N &a, const N &b)
void div (N &rem, const N &a)
void quo (const N &a, const N &b)
void quo (const N &a)
void rem (const N &a, const N &b)
void rem (const N &a)
N & operator/= (const N &rhs)
N & operator%= (const N &rhs)
N operator/ (const N &a, const N &b)
N operator% (const N &a, const N &b)
N div (N &rem, const N &a, const N &b)
N div_exact (const N &a, const N &b)
N quo (const N &a, const N &b)
N rem (const N &a, const N &b)

GCD algorithm selectors

void gcd (const N &a, const N &b)
void gcd (const N &b)
void extended_gcd (N &x, N &y, const N &a, const N &b)
void lcm (const N &a, const N &b)
void lcm (const N &b)

Random

void random (const size_t newsize)
void random2 (const size_t newsize)

Output

limb_t to_int () const
std::string to_binary () const
std::string to_hexadecimal () const
std::string to_decimal () const
std::string to_english () const
void write_english (std::ostream &out) const
std::ostream & operator<< (std::ostream &out, const N &n)

Basic algorithms

void reserve_small (size_t newsize)
void reserve_large (size_t newsize)
void resize_small (size_t newsize)
void resize_large (size_t newsize)
void truncate_large (size_t newsize)
void normalize_large ()

Binary algorithms

size_t two_multiplicity_large () const
size_t two_multiplicity_small () const
void left_shift_large (const N &a, unsigned int count)
void left_shift_small (const limb_t a, unsigned int count)
void left_shift_large (unsigned int count)
void left_shift_small (unsigned int count)
void right_shift_large (const N &a, unsigned int count)
void right_shift_small (const limb_t a, unsigned int count)
void right_shift_large (unsigned int count)
void right_shift_small (unsigned int count)

Addition algorithms

void add_carry_small (const limb_t carry=1)
void add_carry_large (const limb_t carry=1)
void add_large_large (const N &a, const N &b)
void add_large_small (const N &a, const limb_t b)
void add_small_small (const limb_t a, const limb_t b)
void add_large_large (const N &a)
void add_large_small (const limb_t a)
void add_small_large (const N &a)
void add_small_small (const limb_t a)
void add_one_large ()
void add_one_small ()

Substraction algorithms

void sub_large_large (const N &a, const N &b)
void sub_large_small (const N &a, const limb_t b)
void sub_small_small (const limb_t a, const limb_t b)
void sub_large_large (const N &a)
void sub_large_small (const limb_t a)
void sub_small_small (const limb_t a)
void sub_one_large ()
void sub_one_small ()

Multiplication algorithms

void mul_large_large (const N &a, const N &b)
void mul_large_small (const N &a, const limb_t b)
void mul_small_small (const limb_t a, const limb_t b)
void mul_large_large (const N &a)
void mul_large_small (const limb_t a)
void mul_small_large (const N &a)
void mul_small_small (const limb_t a)

Addmul and submul algorithms

void addmul_large_large (const N &a, const limb_t b)
void addmul_large_small (const limb_t a, const limb_t b)
void addmul_small_large (const N &a, const limb_t b)
void addmul_small_small (const limb_t a, const limb_t b)
void submul_large_large (const N &a, const limb_t b)
void submul_large_small (const limb_t a, const limb_t b)
void submul_small_large (const N &a, const limb_t b)
void submul_small_small (const limb_t a, const limb_t b)

Division algorithms

void exact_div_large_large (const N &a, const N &b)
void exact_div_large_small (const N &a, const limb_t b)
void exact_div_small_small (const limb_t a, const limb_t b)
void exact_div_large_large (const N &b)
void exact_div_large_small (const limb_t b)
void exact_div_small_small (const limb_t b)
void div_large_large (N &rem, const N &a, const N &b)
void div_large_small (N &rem, const N &a, const limb_t b)
void div_small_large (N &rem, const limb_t a, const N &b)
void div_small_small (N &rem, const limb_t a, const limb_t b)
void div_large_large (N &rem, const N &b)
void div_large_small (N &rem, const limb_t b)
void div_small_large (N &rem, const N &b)
void div_small_small (N &rem, const limb_t b)
void quo_large_large (const N &a, const N &b)
void quo_large_small (const N &a, const limb_t b)
void quo_small_large (const limb_t a, const N &b)
void quo_small_small (const limb_t a, const limb_t b)
void quo_large_large (const N &b)
void quo_large_small (const limb_t b)
void quo_small_large (const N &b)
void quo_small_small (const limb_t b)
void rem_large_large (const N &a, const N &b)
void rem_large_small (const N &a, const limb_t b)
void rem_small_large (const limb_t a, const N &b)
void rem_small_small (const limb_t a, const limb_t b)
void rem_large_large (const N &b)
void rem_large_small (const limb_t b)
void rem_small_large (const N &b)
void rem_small_small (const limb_t b)

GCD algorithms

void gcd_large_large (const N &a, const N &b)
void gcd_large_small (const N &a, const limb_t b)
void gcd_small_small (const limb_t a, const limb_t b)
void gcd_large_large (const N &b)
void gcd_large_small (const limb_t b)
void gcd_small_large (const N &b)
void gcd_small_small (const limb_t b)

GCD operators

N gcd (const N &a, const N &b)

Detailed Description

Arbitrarily large natural numbers (positive integers including zero).

N is designed to be a general purpose Arbitrary-precision integer (also known as bignum) class. "Integer" in this case means positive integers including zero.

Internally the number is represented by an array of "limbs", which are 32 or 64 bit long on modern cpu's. The array can be accessed with the function limbs(). The limbs are stored from least significant to most significant.

A optimization is done when the number fits in a single limb (the number is 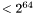$ < 2^{64} $). In this case there will be no heap allocations done and alle calculations will be done entirely on the stack, as long as they don't exceed the limb size.

For numbers of multiple limbs the class relies on the low-level algorithms of GMP. These are reliable and give near optimal performance on most CPU's.

The design goals of the N class are

Design

Most operations, like addition and multiplication are designed in two parts. The raw algorithms, the algorithm selectors and overloaded operators. All these functions come in two flavors, in place and out of place.

Algorithm selectors

Let's take multiplication as an example. The algorithm selectors are:

The first is the out-of-place flavor, it sets the current N (the "this" object) to the product of a and b. For example, to store the product of x and y in z you could write: z.mul(a, b) The three variants are type-overloaders. They allow you to use litteral numbers as arguments: z.mul(a, 5).

The last three are in-place algorithms, to multiply x by y and store the result in x you could write x.mul(y).

The algorithm selectors are called "selectors" because they look at the size of the numbers and select the appropriate algorithm. mul(a, b) for example, will do a direct calculation if both numbers are of native cpu size, otherwise it will call an appropriate GMP function.

All the selectors are marked inline to benefit from constant propagation, if this is properly done the selection is made at compile time and the overhead vanishes.

Overloaders and convenience functions

Limitations

The size is only limited by the available memmory of the computer. Theoretically, for a 64-bit machine, the maximum integer is

\[ 2^{64 \cdot 2^{64}} \approx 10^{3.6 \cdot 10^{20}} \mbox{.} \]

In practice no machine will get close to this limit. Experiments on my 2GB ram 64-bit laptop give an upper bound of approximately

\[ 2^{268435456} \approx 10^{80807124} \mbox{.} \]

Calculations should be safe until around a milliamilliatillion 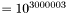$ = 10^{3000003}$.

examples

N mersenne;
mersenne = 1;
mersenne <<= 32582657;
mersenne -= 1;
mersenne.write_language(cout);

Algorithms

Warning:
These functions give direct access to the algorithms used in N. They bypass all the safety checks done in the normal operations, calling them incorrectly will result in chaotic and undefined behavior and will cause hard to track bugs in the entire internet! (No, seriously, just watch out, okay?)
The actual calculations are done in the algorithms. The function names are structured as mul_<size of operant a>_<size of operant b> where the size of an operant is "small" when it is only a single limb, and "large" when it is at least two limbs.

Again, there are two flavors, in-place and out-of-place. The out of place flavors come in four variants or three when the operation is commutative. In-place operations are never commutative so they always come in four variants.

Todo's

Todo:
32 bit support
Todo:
gmp nails support
Todo:
Use proper exceptions
Todo:
Fast exact division see mpz_divexact
Feature requests:

Todo:
Square, inplace and outofplace
Todo:
num_bits() = floor(log2(n));
Todo:
is_divisible(N& n)
Todo:
divides(N& n) = n.is_divisible(*this)
Todo:
is_congruent(N& a, N& modulus)
Todo:
pow(N& exponent)
Todo:
pow_mod(N& exponent, N& modulus)
Todo:
root(N& remainder, limb_t n)
Todo:
sqrt
Todo:
is_perfect_power()
Todo:
is_perfect_square()
Todo:
is_prime(int reps = 10)
Todo:
nextprime();
Todo:
Extended GCD
Todo:
invert(N& modulus)
Todo:
jacobi, legendre, kronecker, factorial

Definition at line 161 of file N.h.

Member Typedef Documentation

typedef mp_limb_t limb_t

The type of the digits in the large number.

Definition at line 168 of file N.h.

typedef long unsigned int size_t

The type of the arrays size.

Definition at line 171 of file N.h.

Member Function Documentation

void reserve ( size_t  newsize  )  [inline]

Reserve space for newsize limbs.

Allocate memory for newsize limbs, if newsize is zero, all memory is deallocated and limb can be used safely.

Parameters:
newsize The required size of the number. newsize is measured as number of limbs - 1.
See also:
size
Postcondition:
The N's value is undefined.

The N is not normalized.

Definition at line 554 of file N.h.

Referenced by N::gcd_large_large().

void resize ( size_t  newsize  )  [inline]

Resize the integer to use newsize limbs.

Contrary to reserve this function preserves the value of the integer. This means it is not possible to decrease the size of the integer, doing so will result in an exception.

The number is padded with leading zero's to fit the new size.

Parameters:
newsize The size the N should become.
Postcondition:
The N is not normalized if newsize > size.

Definition at line 583 of file N.h.

void truncate ( size_t  newsize  )  [inline]

Truncate the integer to use newsize limbs.

Just like resize, this function changes the numbers of limbs while perserving the value. The difference is that truncate will allow shrinking the number by throwing away the most significant limbs until the new size is reached.

If newsize > size the number is padded with leading zero's to fit the new size. If newsize < size the number is the most significant limbs are thrown away.

Parameters:
newsize The size the N should become.
Postcondition:
The N is not normalized if newsize > size.

Definition at line 617 of file N.h.

Referenced by N::gcd_large_large().

void normalize (  )  [inline]

Normalize the number.

This function normalizes the N by removing all leading zero's in the limb representation. If the result is a single limb the N will become small.

Most algorithms have maximal performance when N is normalized. All algorithms are designed to perserve normalization unless otherwise noted.

Definition at line 648 of file N.h.

size_t two_multiplicity (  )  const [inline]

Returns the number of trailing zeros in the binary representation.

Definition at line 818 of file N.h.

void truncate_large ( size_t  newsize  ) 

Precondition:
newsize < size

size > 0

Definition at line 60 of file N.Basic.cpp.

References N::data, N::limb, and N::size.

void gcd_large_large ( const N &  a,
const N &  b 
)

Todo:
Detect small numbers a_odd and/or b_odd and use small algorithms

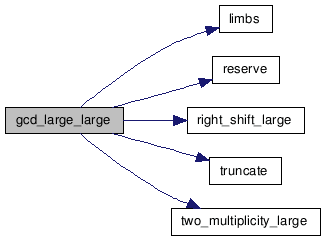
Definition at line 7 of file N.GCD.cpp.

References N::limbs(), N::reserve(), N::right_shift_large(), N::size, N::truncate(), and N::two_multiplicity_large().

Here is the call graph for this function:

Friends And Related Function Documentation

size_t max ( const size_t  a,
const size_t  b 
) [friend]

Returns the greatest of two N::size_t's.

Definition at line 535 of file N.h.

Member Data Documentation

const int bits_per_limb = 8 * sizeof(limb_t) [static]

Constant representing the number of bits in a limb_t.

Definition at line 174 of file N.h.

size_t size

The number of limbs minus one.

Definition at line 177 of file N.h.

Referenced by N::gcd_large_large(), and N::truncate_large().

limb_t limb

If size is zero then limb contains the entire integer.

Definition at line 183 of file N.h.

Referenced by N::truncate_large().

limb_t* data

Array of limbs representing the integer. If size >= 1 then data will contain an allocated array of size + 1 limbs representing the integer from least significant limb data[0] to the most significant limb data[size].

Definition at line 190 of file N.h.

Referenced by N::truncate_large().

The documentation for this class was generated from the following files:

Copyright © 2007-2008 Remco Bloemen.

Generated on Tue Jan 22 17:35:31 2008 for symbolism by doxygen 1.5.4

Hosted by SourceForge.net Logo